Matura 2011: Arkusze i rozwiązania z matematyki - poziom rozszerzony
Znamy już wszystkie zadania, jakie pojawiły się na maturze z matematyki! Nasi eksperci przygotowują proponowane rozwiązania z poziomu rozszerzonego!

Poniżej znajdziecie zaproponowane przez naszych matematyków odpowiedzi. Propozycje rozwiązań są dodawane na bieżąco (odświeżajcie stronę).
POZIOM ROZSZERZONY
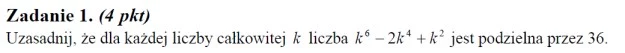

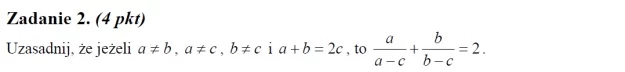
Ad. 2. L = [a(b-c)+b(a-c)] / [(a-c)(b-c)] = (ab-ac+ba-bc) / [(a-c)(b-c)] = [2ab-c(a+b)] / [(a-c)(b-c)] = = [2ab-c(2c)] / [ab-ac-cb+c^2] = 2[ab-c^2] / [ab-c(a+b)+c^2] = 2[ab-c^2] / [ab-c(2c)+c^2] = 2[ab-c^2] / [ab-c^2] = 2 = P

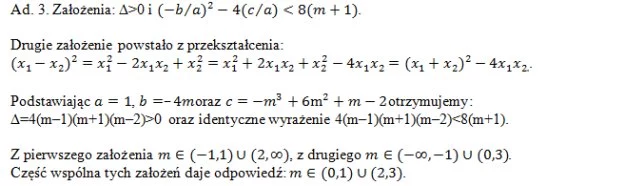
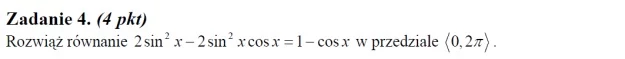
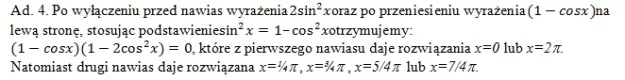

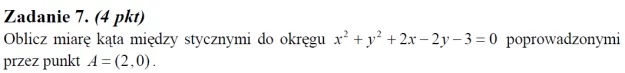





Ad. 9. Komentarz:
Przyjęto założenie, że skoro "występują dwie dwójki i występują trzy trójki", to:
a) nie występuje więcej dwójek ani więcej trójek,
b) nie występują inne cyfry w większej liczebności, niż 1 (powtarzające się).
Są to założenia domniemane, które są jedną z metod interpretacji zadania (zapewne również poprawnego, bo treść nie jest precyzyjna).
A dalej już zgodnie z rozwiązaniem: jeśli ze zbioru siedmioelementowego wybierzemy trzy cyfry bez powtórzeń, to będzie 35 możliwości.
Wybrane trzy cyfry wraz z "dwiema dwójkami i trzema trójkami", to osiem cyfr, które można ułożyć na 3360 różnych sposobów.
Zatem mamy 117600 takich liczb ośmiocyfrowych. Druga i trzecia metoda rozwiązania zadania (ze względu na niejednoznaczność treści - brakuje słów "dokładnie", "tylko" lub "co najmniej") opierają się odrzuceniu pierwszego założenia (czyli może występować więcej dwójek lub trójek) lub drugiego założenia (czyli inne liczby mogą się powtarzać) albo obu naraz. Wtedy można uzyskać odpowiedzi 408 240 możliwości lub 192 080 możliwości.
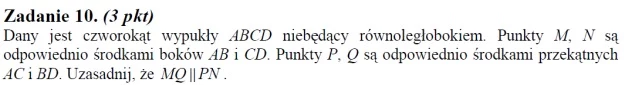
Ad. 10. Najkrótszy sposób dowodzenia równoległości odcinków MQ i PN opiera się na skorzystaniu z twierdzenia, że odcinek łączący połowy ramion dowolnego trójkąta jest równoległy do podstawy i równy jej połowie. Na potrzeby dowodu wystarczy pierwsza cecha wskazanego twierdzenia, a więc fakt, że odcinek MQ jest równoległy do boku AD tego czworokąta, bo łączy połowy ramion trójkąta ABD. Analogicznie odcinek PN jest również równoległy do boku AD tego czworokąta, bo łączy połowy ramion ACD. Skoro więc MQ || AD oraz PN || AD, to MQ || PN.



Tegoroczni maturzyści są drugim rocznikiem, po ponad 25-letniej przerwie, który obowiązkowo zdaje matematykę.
Chęć zdawania egzaminu na poziomie rozszerzonym zadeklarowało 15 proc. tegorocznych maturzystów. Egzamin na poziomie podstawowym potrwa 170 minut, a na poziomie rozszerzonym - 180 minut.
W ubiegłym roku, gdy po raz pierwszy przeprowadzano obowiązkowy egzamin z matematyki na poziomie podstawowym, wymagany próg minimum 30 proc. punktów koniecznych do zdania egzaminu przekroczyło 87 proc. maturzystów. Uzyskany przez nich średni wynik to 58 punktów na 100 możliwych.
Z kolei podczas listopadowego egzaminu próbnego z matematyki próg 30 proc. punktów przekroczyło tylko 64 proc. tegorocznych maturzystów.









